Let’s pretend we have two sets.
The first set will be the first ten positive whole numbers.
The second will be the first ten prime numbers.

>>> set1 = set(range(10))
>>> set2 = {1,2,3,5,7,11,13,17,19,23}

Union

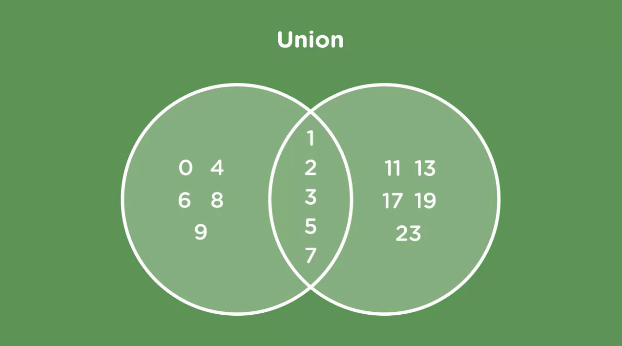
The first operation to talk about is union. This is the combination of two or more sets.
But since sets are unique, we wouldn’t get multiple ones, or fives, or anything.

>>> set1.union(set2)
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19, 23}

>>> set1 | set2
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19, 23}

Difference

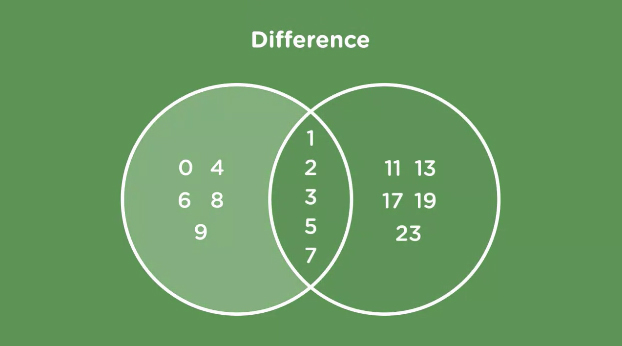
This operation finds everything that’s in the first set, but not in the second.

>>> set1.difference(set2)
{0, 4, 6, 8, 9}
>>> set2.difference(set1)
{11, 13, 17, 19, 23}

>>> set1 - set2
{0, 4, 6, 8, 9}
>>> set2 - set1
{11, 13, 17, 19, 23}

Symmetric Difference

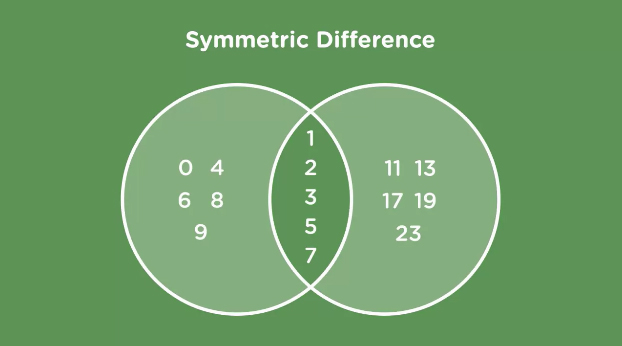
This is everything that is unique to either set.
So, no shared numbers. Sorry primes below ten.

>>> set2.symmetric_difference(set1)
{0, 4, 6, 8, 9, 11, 13, 17, 19, 23}

>>> set1 ^ set2
{0, 4, 6, 8, 9, 11, 13, 17, 19, 23}
>>> set2 ^ set1
{0, 4, 6, 8, 9, 11, 13, 17, 19, 23}

Intersection

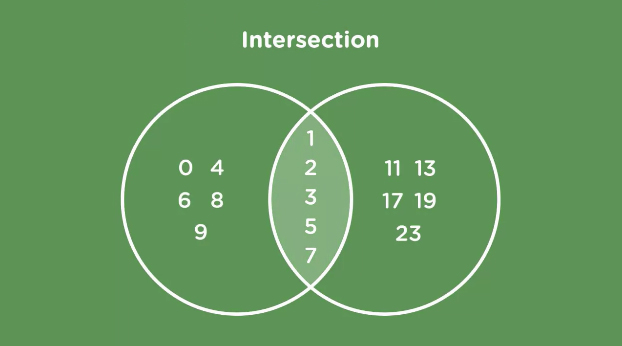
Gives a new set of all items that are in both sets.
The intersection of these two sets gives us only the primes below ten.

>>> set1.intersection(set2)
{1, 2, 3, 5, 7}

>>> set1 & set2
{1, 2, 3, 5, 7}